This article explains how game theory in risk management can be used to address an identified risk.
 Many liked the post on Risk and Game Theory with Ruth Fisher (my co-author on the piece). We were asked for more, especially an example or two.
Many liked the post on Risk and Game Theory with Ruth Fisher (my co-author on the piece). We were asked for more, especially an example or two.
As with the last post, I will set the stage and then Ruth will share how game theory can be used.
This is more an article than a blog post, as the explanation of how to solve the problem takes a while. It is also, at times, complex. If you want, you can skip some of the technical stuff (equations and so on).
The main thing, for me, is to understand that the optimal action to address the identified risk has to consider not only the perspective of the ‘owner’ of the risk (Management) but also the perspectives of the other two parties (the Employees and Competitors). Game theory factors how the other parties will react into the process of making the decision of how to respond to the risk.
Your comments and reactions are welcome.
One of the risks identified by many organizations as significant and included in the risk disclosures required in corporate filings, such as the annual and quarterly filings with the U.S. Securities and Exchange Commission, is the loss of key personnel.
Here is an extract from IBM’s 2016 Annual Report on Form 10-K:
The Company Depends on Skilled Personnel and could be impacted by the loss of Critical Skills: Much of the future success of the company depends on the continued service, availability and integrity of skilled personnel, including technical, marketing and staff resources. Skilled and experienced personnel in the areas where the company competes are in high demand, and competition for their talents is intense. Changing demographics and labor work force trends may result in a loss of or insufficient knowledge and skills. In addition, as global opportunities and industry demand shifts, realignment, training and scaling of skilled resources may not be sufficiently rapid or successful. Further, many of IBM’s key personnel receive a total compensation package that includes equity awards. Any new regulations, volatility in the stock market and other factors could diminish the company’s use, and the value, of the company’s equity awards, putting the company at a competitive disadvantage or forcing the company to use more cash compensation.
Assessing this risk is not simple.
Arguably, the risk is different for different groups of personnel such as:
- The CEO
- The direct reports to the CEO
- Their direct reports
- Middle management
- Individuals with critical skills or knowledge, such as those leading innovation and product development
- Other personnel where the loss would be significant but replacements might be found within a reasonable period
So let’s focus on the risk of losing people in the critical skills or knowledge category.
IBM’s discussion focuses on losses due to others offering greater compensation. No mention is made of losses due to employee morale problems and so on – so I will focus on compensation.
At first blush, this may seem fairly straightforward. But in real life identifying the risk, assessing its level, and evaluating whether it is acceptable is only a start.
It can be quite complicated, even for what seems a simple risk like the potential to lose people, to figure out what to do about it.
Most risk managers, unfortunately, don’t pay enough attention to the response to risk.
Here’s a hypothetical situation:
- The company is very concerned about the loss of critical personnel in its product development team, in particular those working on the next generation product slated to be released in the next year. They have lost staff to their competitors at an unacceptable rate and believe that further losses would harm their ability to maintain their technological edge in the market and introduce a product on time that will excite customers at a reasonable price
- It is possible that staff members could take their knowledge and information about the company’s products (its intellectual property) to a competitor
- Failing to introduce the next generation product into the market on time could be devastating to revenue, market share, customer retention, share price, and so on
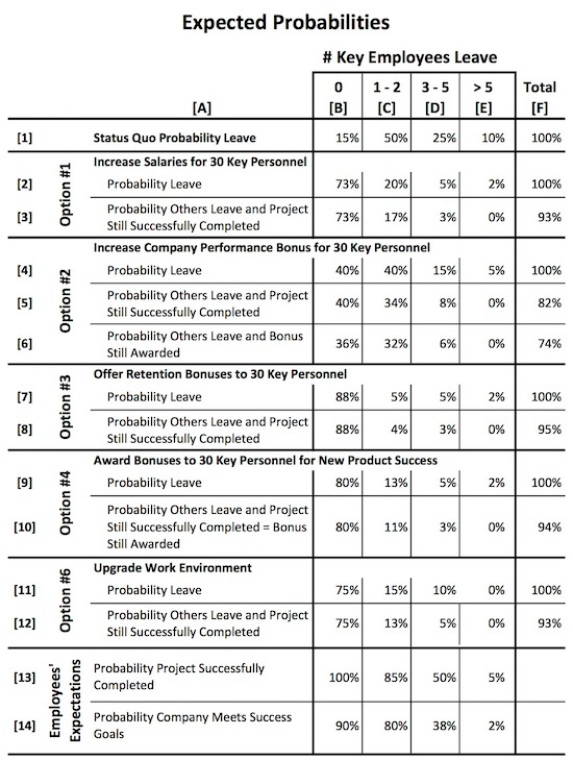
- If no action is taken, management assesses the likelihood of losing key personnel (30 are working on the next generation product out of a population of 50 engineers) as:
- No losses in the next 12 months: 15%
- 1-2 engineers: 50%
- 3-5 engineers: 25%
- >5 engineers: 10%
- The average potential loss (considering the effect on revenue, customer satisfaction, market share and other goals) for each of these scenarios is in a range:
- No losses: $0
- 1-2 engineers: $1 million
- 3-5 engineers: $10 million
- >5 engineers: $50 million
- The risk is seen as unacceptable and action is needed – as long as the cost is less than the reduction of risk achieved
- Management believes that the compensation package (salary, benefits, and bonus) is competitive. It is in line with what they believe others are offering. However, that has not stopped staff from leaving – presumably for more money
- One option is to increase salaries for the 30 key personnel at a cost of $450,000 per annum. However, that may create a problem with other personnel in equivalent positions who have similar skills and experience
- Another is to increase bonus awards for the 30, also at a cost of about $450,000. However, those are linked to corporate performance and are not assured. Competitors may offer hiring bonuses and higher salaries
- A third option is to offer retention bonuses to the 30 (at a similar cost). However, if other team members (such as in Quality and Inspection) leave, that may also derail product development
- Bonuses could be awarded in a similar amount for successful completion of the new product. However, individuals on other teams could feel slighted and leave. That would have a detrimental effect on customer satisfaction and longer term goals: the other engineers support customer implementations, provide maintenance, and are working on the products planned for release in 2019
- There is a limit to the company’s ability to increase compensation packages – the strain it would put on profit margins and corporate earnings targets. The risk of missing those targets would be affected by increased salaries or bonuses
- Another option is to leave compensation where it is but dedicate Human Resources personnel to monitoring morale in the engineering unit. In addition, invest $500,000 in software that will monitor employee (internal) social media posts and messages. However, there is a risk to morale if the engineers find out about the monitoring
- An employee has suggested upgrading the engineers’ work environment with expensive coffee machines, free soft drinks, a running track, a foosball machine, access to a gym, and free upscale meals in the cafeteria. This would cost at least $250,000 per year and would be available to all employees, not just the engineers
- The Human Resources manager suggested making employee retention a key factor in middle management’s performance appraisal. But this is not considered likely to make a significant difference to the level of risk.
- To empower middle management in retaining key personnel, upper management has given responsibility to middle management for deciding which option(s) to implement.
So, Ruth, how would game theory help the management team assess each option for addressing this problem and then determine the best approach? How would it bring into the equation the reactions of the engineers, other employees, and competitors?
Ruth is going to pretend to be a consultant that has been hired by management to help them figure out what to do.
They chose her because they recognize that they have to consider how others (competitors and employees) will react to what they choose to do. That is the essence of game theory.
Thanks for the setup, Norman.
Let’s start by defining the players in the game. The players are those individuals, groups, or entities whose actions and payoffs are interconnected.
In the case at hand, the risk is that one player will take an action: the Competition lures the Company’s Key Employee away by offering a higher salary or other incentive; then, a second player reacts to the actions of the first player: one or more Key Employees accept the higher salary and leave the Company to work for the Competition.
The second player’s response to the first player’s action affects the payoff of a third player: Without the Key Employee, the Company is less able to successfully finish the new product on time, and so expected Company profit falls.
The third player thus anticipates the possibility of the actions that might be taken by the first and second players with yet another action: The Company knows that it won’t be able to successfully complete the new product without the Key Employees. So if the Competition offers a Key Employee a higher salary or other incentive to leave, the Company will respond to the Competitor’s action with a counter-action: offering the Key Employee a higher salary, a bonus, or other incentives to stay. The Company may, and this is what I will advise, take one or more pre-emptive actions that will reduce the likelihood that Key Employees will take offers from the Competition.
We see, then, that the actions taken by each of the players—the Company, the Key Employees, and the Competitor—affect the payoffs (profits and compensation) each player receives. These players thus form a game.
Norman’s descriptions yield a configuration of the Employee Retention Game as illustrated in Figure 1:
Figure 1

Expectations of losses
The Company believes Key Personnel on the project team may leave the company to work for Competitors with the probabilities and associated losses to the Company presented in Figure 2.
Figure 2
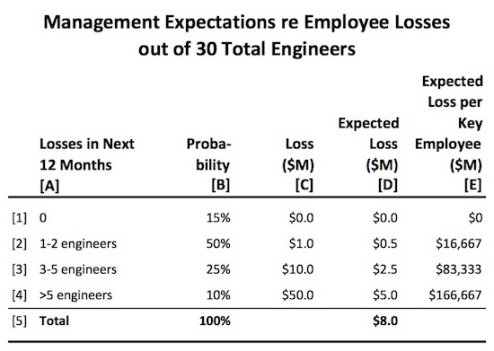
The Company believes that with probability 50%, 1 or 2 Key Personnel on the project team will leave the Company to work for a Competitor (see Figure 3, row [2]). If this happens, the loss to the Company will be around $1 million (column [C]).
That would be painful but tolerable. However, there is an additional 35% possibility of additional losses. Losing more than 5 Key Employees would be catastrophic.
One consultant from a major accounting firm suggested establishing a ‘risk appetite’. But management is not sure that means anything tangible to them. They believe that the right approach, with which I agree, is to understand the options, how they will change the risk at what cost, and then select from them the one or more that make good business sense.
Management options
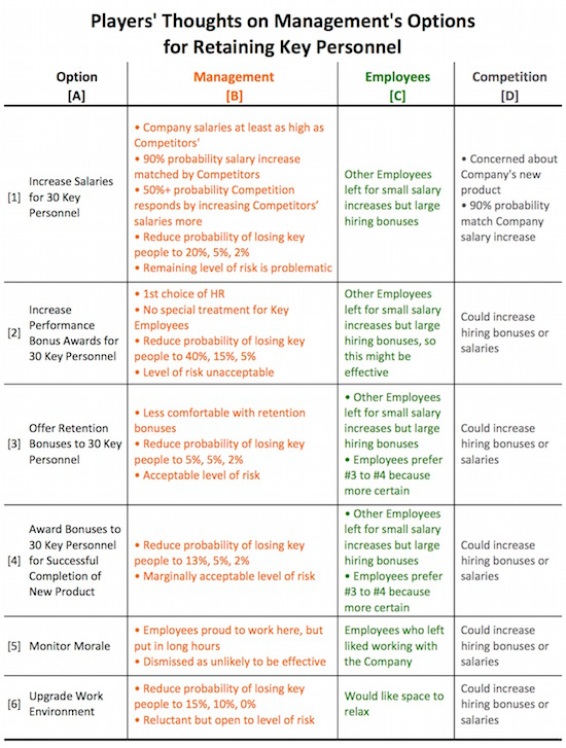
The possible actions identified by Management to prevent Key Employees on the project team from leaving are shown in Figure 3.
Figure 3

The first thing to note is that each option costs less than the $1 million loss projected if 1 – 2 Key Employees leave.
But we don’t yet know how likely each of the options is to succeed.
Talks with the company about employee satisfaction
Before attempting any further analysis, I need to talk to both Management and the Project Team.
A conversation with the Management Team, including the Human Resources representative, tells me:
- The Company believes it is already paying towards the high end of the salary range for these engineers. Surveys conducted by Human Resources indicate that the Company is actually paying the same or more than its competitors.
- The Company recently completed an employee survey. Morale seems to be high and most employees say they are proud to be working there.
- Management is open to paying bonuses for completing the project on time and on budget, but it is less comfortable with retention bonuses that are not linked to satisfactory completion of the project.
- Neither Management nor Human Resources knows much about working conditions at the Competitors. Management does know that its people often have to put in long hours (including weekends) and improvements in working conditions would be within its budget.
- Management is confident that the Competitors are very concerned about the Company’s next generation product. The Competition would be willing to spend a lot of money to derail the project, even if that meant hiring people they didn’t need away from the Company. For that reason, Management is 90% confident that any increase in salaries paid by the Company would be matched by competitors.
A separate conversation with the Human Resources person told me that:
- In exit interviews, engineers that have left said they liked their manager – so that is not a problem. They also had enjoyed working for the Company.
- They said that significant hiring bonuses offered by the Competitors were the main reason they were leaving. It was not dissatisfaction with the Company. It was the opportunity to move to a new home, pay for a child’s college tuition, or cover another major cost that was attractive.
I met with a group of Key Employees after that. They told me:
- Overall, they enjoyed working for the Company and were proud of the work they were doing. They were looking forward to completing the project and letting the world see the next generation product.
- They were tired of working many hours although they knew that it was necessary. They all said they needed a space where they could relax on a long day or weekend.
- Friends who had left the Company and joined Competitors were not always happy with the move, but they had been financially stressed. They had only been given small salary increases but substantial hiring bonuses.
The Employees I met with did not admit to actively looking for new jobs and appeared to be happy where they were, even after hearing from—and even visiting—friends who had left.
Assessing the options
I met with the Management Team to assess each of the options in Figure 3.
We quickly dismissed option #5, Monitor Morale, as being very unlikely to prevent anybody from leaving. This might be a viable option for the longer term, especially if combined with other actions. But it would not help enough in the short term, before the project is completed.
Management didn’t like the first option, increasing salaries. They had 90% confidence that the Competitors would at least match the salaries. In fact, Management thought it at least 50% likely that the Competition would respond to the Company’s salary increase by increasing Competitors’ salaries even more. But Employees might see raising salaries favorably. We estimate that raising salaries would reduce the likelihood of losing key people as follows:
- 1-2 people would drop from 50% to 20%
- 3-5 would go from 25% to 5%
- More than 5 would drop from 10% to 2%
However, this remaining level of risk would be problematic.
The second option, increasing bonuses that are tied to corporate performance, was the pick of the Human Resources representative. It wouldn’t make the engineers a group receiving special treatment. But Management estimated this will reduce the likelihood of losing personnel by less:
- 1-2 people would drop to 40%
- 3-5 would now be 15%
- More than 5 would still be high at 5%
The level of risk would remain unacceptable.
The third and fourth options, retention bonuses and bonuses for successful completion of the project, drew mixed reviews. Management prefers option #4 (success bonus) but think Employees would prefer #3 (retention bonus) because it is more certain. They believe #3 will reduce the likelihood of losing personnel to 5%, 5%, and 2% (which is acceptable), and #4 to 13%, 5%, and 2% (which is marginally acceptable).
Management is uncertain how Employees will react to the option of upgrading the work environment. In fact, a couple of Managers think that it might negatively affect productivity. But Human Resources and the other Managers favor the option. They just don’t know how effective it will be.
My discussion with the employees led me to believe they would respond very positively to #6. After discussion, we agreed to estimate that #6 would reduce the likelihood of 1-2 engineers leaving to 15%, 3-5 leaving to just 10%, and the likelihood of more than 5 to practically zero. Management was, again, reluctant but open to a 15% possibility.
A summary of the information gathered on each of the options is presented in Figure 4.
Figure 4
Using the information in Figures 2 and 4, I calculate the probabilities that Key Employees would leave the Company to work for the Competition. These probability distributions are presented in Figures 5A and 5B.
Figure 5A

Figure 5B
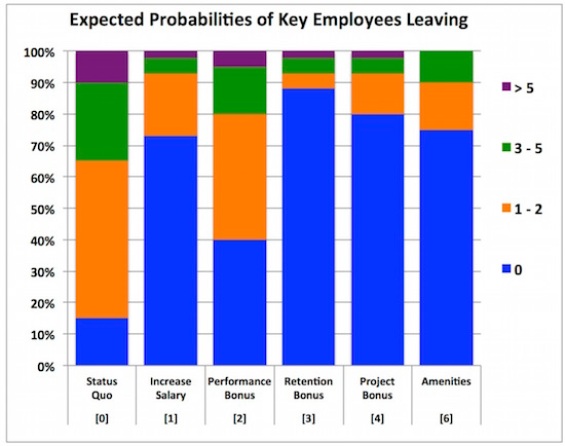
Figures 5A and 5B tell us the likelihoods that certain numbers of Key Employees will leave. Under option #4, for example, there is a 13% chance that 1 – 2 Key Employees will leave. If 1 – 2 Key Employees do leave, however, then what’s the likelihood that the project will still be successfully completed and thus success bonuses be awarded? And in the case option #2, if 1 – 2 Key Employees leave, what’s the likelihood that the Company as a whole will meet its performance goals and thus performance bonuses be awarded? We need another set of probabilities that tell us the likelihoods of project and Company success when some Key Employees leave.
Let’s assume everyone agrees on the probabilities presented in Figures 6A and 6B:
Figure 6A

Figure 6B
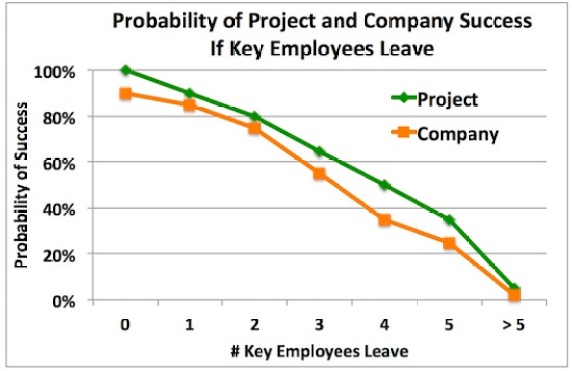
Continuing with the example: Under option #4, there is a 13% chance that 1 – 2 Key Employees leave. If 1 – 2 Key Employees do leave, then, from Figure 6, there is an 85% chance that the project will still be successful and the bonus in option #4 will be granted. There is thus an expected probability of 13% x 85% = 11% that 1 – 2 Key Employees leave and that the remaining Key Employees successfully complete the project and receive their bonuses.
Similarly, under option #2, there is a 40% chance that 1 – 2 Key Employees leave. If 1 – 2 Key Employees do leave, then, from Figures 6, there is an 80% chance that the project will still be successful and the bonus in option #2 will be granted. There is then an expected probability of 40% x 80% = 32% that 1 – 2 Key Employees leave and that the remaining Key Employees will receive Company performance bonuses.
Using the information in Figures 5 and 6, I calculated the expected probabilities of project success and bonuses awarded for each of the options. These expected probabilities are displayed in Figure 7.
Figure 7
Given all these different sets of probabilities, we now need to know which options are best for Management. The best options for Management will depend on how Management thinks Key Employees and the Competition will react to Management’s choice of options.
Technical stuff
It’s time to turn to game theory. It uses expressions like “objective function” and “profit function”.
Let’s start by defining the game. A game includes:
- a set of interconnected players
- a set of actions available to each player, and
- a set of associated payoffs for each player.
We’ve already identified the players in the game, as illustrated in Figure 2.
The next step is to figure out each player’s objective, that is, what he is hoping to achieve. The players’ objectives help us understand two things. First, players’ objectives tell us where they are trying to go, and thus which actions they are likely to take in different situations. Second, player’s objectives (more accurately, their objective functions) tell us how to translate or convert a set of payoffs into an aggregate measure of value. Would a player rather have an apple and two oranges or two oranges and an apple? Similarly, in Figure 5, would a Key Employee prefer the distribution of probabilities under option #1 or option #2? With such a measure of value we can compare different bundles of payoffs received under different scenarios and determine which of the bundles players will prefer.
In the game at hand, the objective of the Company is to reduce the risk of project and Company failure due to key employees leaving to acceptable levels as cost effectively as possible. [While a risk manager may talk about reducing risk to acceptable levels, operating managers talk about achieving a successful outcome – ndm.]
The objective of the Employees is generally to earn money. But Employees also want job satisfaction, which can mean working in a friendly environment, being given ample responsibilities, being recognized for one’s accomplishments, and so on. Employees also enjoy an attractive work environment. Free food and beverages are nice, as well as places to relax and unwind.
The Competitor’s objective for the game at hand is to hire away Company Employees to improve the Competitor’s probability of success, while derailing the Company’s probability of project success.
The actions available to each player are the options each player can take to achieve his objective. The actions available to the Company are the options listed in Figure 4. Key Employees can either stay with the Company or leave to work for the Competition. And the actions available to the Competition are to offer Key Employees salaries and bonuses to leave the Company and work for the Competition.
And finally, the payoff received by each player is the final benefit—product success, compensation, job satisfaction, profit, etc. —he gets when each of the players in the game take an action. Recall that our situation here forms a game because each player’s payoff is affected by the actions the other players take.
This is what I can deduce so far for each of the players:
Middle management
Objectives: Minimize the likelihood of the project failing or being delayed while maintaining the line on cost. The project will be less likely to fail if fewer Key Employees leave to join the Competition.
Possible Actions: Award all or select Team Members increased compensation, monitor morale, and/or upgrade work environment.
Payoffs: Corporate success and personal compensation depend on the success of the project.
Objective Function: The objective function that Middle Management (as proxy for the Company) seeks to optimize looks something like this:
Choose Comp_Keyi to:

Where:
Exposure0 is the Company’s exposure to risk under the status quo, $8 million (see Figure 2, row [5]);
Exposure(Comp_Keyi, Comp_Keyi´) is the exposure to risk the Company faces if the Company offers Key Employee i compensation Comp_Keyi and the Competition offers him Comp_Keyi´;
Prob_Success(Comp_Keyi, Comp_Keyi´) is the probability of project or Company success if the Company offers Key Employee i Comp_Keyi and the Competition offers him Comp_Keyi´.
Management must figure out which compensation or morale boosters will be most effective at reducing the Company’s exposure to risk by convincing Key Employees not to leave to work for the Competition.
Key team members
Objective: Optimize job satisfaction. Compensation is a secondary but important factor: people are more likely to leave due to poor compensation than incented to stay or leave by high compensation. The work environment can be a significant contributor to job satisfaction.
Possible Actions: Choose to remain with the Company or to switch to a Competitor.
Payoffs: Choice of (i) employer, (ii) compensation, and (iii) pride in the new product determine job satisfaction.
Objective Function: The objective function that each Key Employee i seeks to optimize looks something like this:
Choose to stay with the Company or leave and work for the Competition to:
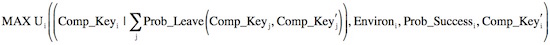
Where
Ui(•) is the total job satisfaction (i.e., utility) for Key Employee i;
Comp_Keyi is the extra compensation or morale booster received by Key Employee i;
![]() … is the extra compensation Key Employee i expects to receive, given the probability other Key Employees j may leave, causing the new project to fail;
… is the extra compensation Key Employee i expects to receive, given the probability other Key Employees j may leave, causing the new project to fail;
Environi is the value Key Employee i receives from a good work environment;
Prob_Successi is the satisfaction Key Employee i receives from successfully launching a new product, given the Key Employee’s estimate of the probability of project success;
Comp_Keyi´ is the extra compensation or morale booster for Key Employee i if he leaves and works for the Competition.
Employees care about:
- (i) Their expected compensation (including success bonuses), given the total number of other Key Employees they expect to leave and work for the Competition. Employees will be alert to potential defections of other Key Employees, because that will hamper the performance of the team, the probability the project and Company will succeed, and thus their expected success bonuses.
- (ii) The work environment.
- (iii) The personal satisfaction in a job well done – completion of the new product. I’m assuming that Key Employees have a chance of successfully completing the project if they stay with the Company, but not if they leave and work for the Competition.
- (iv) The compensation they can expect to earn if they defect to the Competition.
Let’s approximate the value to Key Employee i of a good work environment as some fraction or multiple, g, of his compensation award: Environi = g x Comp_Keyi. Based on the probabilities in Figure 7, it appears that Key Employees value an improved work environment relatively highly, about as much as they value a salary increase (option #1).
Let’s also approximate the value to the personal satisfaction he gets from successfully completing the new product as some fraction or multiple, l, of his compensation award.
In this case a decision function for Key Employees might look something like this:
Figure 8

If the value of the equation in Figure 8 is positive, then the Key Employee will choose to stay with the Company. Conversely, if the value of the equation in Figure 8 is negative, then the Key Employee will choose to leave the Company and work for the Competitor.
Notice that both components of the value received from the Company occur with some risk, while the value component for the Competitor is certain. The Company is thus at more of a disadvantage – that is, Key Employees are more likely to accept the Competition’s no-risk offer of compensation – when Key Employees are more risk averse.
Notice also that the Company is at more of an advantage – that is, Key Employees are more likely to stay – when Key Employees get more satisfaction from successfully completing a product.
These two tendencies of Key Employees – risk aversion and job satisfaction – are a general property of utility functions, not just a byproduct of the form of the function chosen here.
Competitors
Objective: Hire employees to optimize performance of teams relative to that of the Competition.
Possible Actions: Use compensation packages to recruit team members away from current employers.
Payoffs: Profits are higher when succeed in recruiting more and better employees.
Objective Function: The objective function the Competition wants to optimize looks something like this:
Choose Comp_Keyi´ to:

Where:
Comp_Keyi´ is the extra compensation paid to Key Employee i to convince him to leave the Company and work for the Competition;
COMP´ is the upper limit on expenditures the Competition can afford to spend to keep Key Personnel from leaving.
The Competition’s objective function is essentially the opposite of the Company’s: The Company essentially wants all its Key Employees to stay and work for the Company. The Competition wants the Company’s Key Employees to leave and work for the Competition. Recruiting Key Employees away from the Company simultaneously strengthens the Competition while it weakens the Company. Double Whammy!
Outcome of the game
Management’s expected payoffs
Let’s start with Management’s expected payoffs under the different options, presented in Figure 9. Note that we previously discarded option 5 as unlikely to prevent employees from leaving.
- Expectations about the Company’s exposure in the current situation, rows [1] and [7], are taken from Figure 2.
- The expected probabilities of Key Employees leaving, rows [2] – [6] in columns [B] – [E], are taken from Figure 5A.
- The potential exposure to the Company, columns [F] – [J], is the product of the probability Key Employees leave, columns [B] – [E], times the loss to the Company if Employees do leave, row [7].
- Column [J] provides the total exposure of the Company for each option, the sum of columns [F] – [I].
- Column [K] provides the reduction in exposure of each option (column [J]) relative to the status quo in row [1].
- Column [L] is the cost to the Company of each option, taken from Figure 3.
- Column [M] is the probability the cost in column [L] will be realized, taken from Figure 7, column [F].
- Column [N] is the expected cost to the Company of each option, column [L] times column [M].
- And The net value to the Company of each option, column [O], is the difference between the savings in exposure realized by each option and its associated cost.
Figure 9
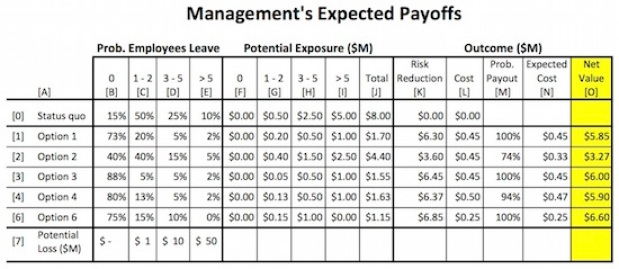
The order of preference for the Company, based on the net values of the different options, is:
Option #6 > Option #3 > Option #4 > Option #1 > Option #2
Key employee’s expected payoffs
Next, we consider the expected payoffs to Key Employees under each option, using the Key Employees’ utility function in Figure 8. The two big issues for Employees are:
- (i) The degree to which they don’t like risk, and
- (ii) The degree to which they do like job satisfaction.
Figures 10A and 10B compare the total utility of Key Employees under four assumptions:
Column [G]: Indifferent to Risk, Care Less about Job Satisfaction
Column [H]: Indifferent to Risk, Care More about Job Satisfaction
Column [I]: Don’t Like Risk, Care Less about Job Satisfaction
Column [J]: Don’t Like Risk, , Care More about Job Satisfaction
Figure 10A
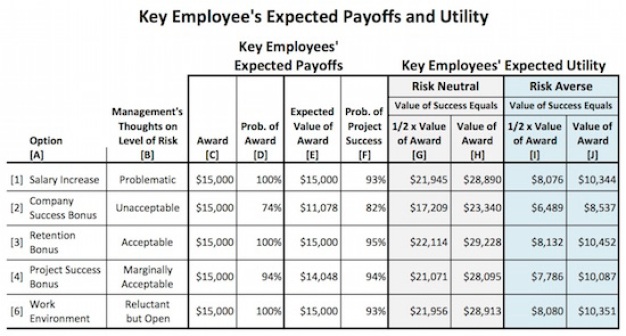
Figure 10B
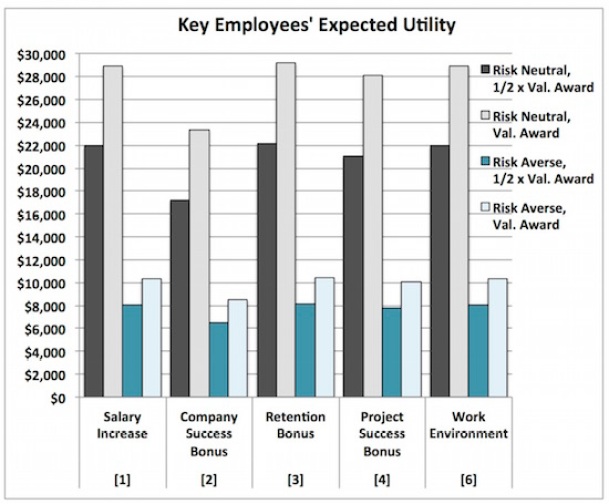
The comparisons of Key Employees’ utilities across forms (columns [G] – [J] in Figure 10A) tell us:
- The rankings of the options are the same across all four forms of Key Employees’ utility functions. The total expected value, however, differs across the configurations.
Option #3 > Option #6 > Option #1 > Option #4 > Option #2
Based on the comparisons in Figures 10A, we can also surmise that if Key Employees prefer[1]:
- Less risk in their compensation awards (column [D]), then they will likely stay under options #1, #3, #4, and #6.
- Larger expected awards (column [E]), then they will stay under options #1, #3, #6, and perhaps #4.
- Job satisfaction from successful project completion (column [F]), then they will likely stay under options #1, #3, #4, and #6.
And if Key Employees think other Key Employees prefer:
- Less risk in their compensation awards, then they will think other Key Employees are more likely to leave under options [2] and [4] than the numbers in the table suggest. In this case, both the expected value of the award (column [E]) and the probability of success (column [F]) would be lower than indicated by the numbers in the table.
- Larger expected awards, then they will leave under options #2 and perhaps #4.
- Job satisfaction from successful project completion, then they will leave under option #2.
Conclusions
The ordering of preference across options for the two sets of players is presented in Figure 11.
Figure 11

The highest value choice for Management is option #6. However, Management is ‘reluctant but open’ to option #6. At the same time, option #6 is the second most desirable choice for Key Employees.
The second highest value choice for Management is option #3, and Management thinks this is an acceptable option. At the same time, option #3 is the preferred choice of Key Employees.
My advice to Management would be to choose option #3 over option #6 for two reasons in particular:
- Management thinks option #3 is acceptable, but it is reluctant to choose option #6.
- It’s possible Management is underestimating the probability that employees will leave. In other words, choosing Option #3 hedges against the possibility Management underestimated the probability employees would leave.
[1] The probabilities of project or Company success in columns [C] and [E] depend on the estimated probabilities in Figure 6. If some Key Employees think the estimates in Figure 6 are too high, then those Employees will have lower values for columns [C] and [E] than those presented in Figure 10A. Correspondingly, those Employees would be more likely to leave the Company and work for the Competition than columns [C] and [E] suggest.
Addendum
Here is the chart requested by Nik

- What is quality internal auditing? - April 17, 2024
- Conflicting research and thoughts on ESG - March 20, 2024
- Useful ethics training for internal auditors - February 21, 2024

